Ruut

Dit Woort hett noch annere Bedüden: kiek dorför ünner Ruut (mehrdüdig Begreep).

Bispill för en Ruut

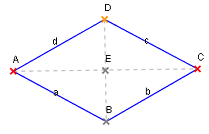
In de Geometrie is en Ruut (ok Rhombus) en Veereck, wonehm alle veer Sieden liek lang sünd.

De Ruut hett disse Egenschoppen:

• De beiden Diagonalen sünd Symmetrieassen.
• De twee Diagonalen staht lootrecht openanner.
• De Winkels, de sik gegenöver liggt, sünd liek groot.
• Naverwinkels sünd tosamen 180° groot.
• De Binnenwinkels warrt vun de Diagonalen halbeert.
• Dat gifft en Binnenkreis.

De Ruut is en Spezialfall vun den Draken, vun’t Parallelogramm un ok vun’t Trapez. Annersrüm gifft dat ’n spezielle Ruut, de ’n Quadrat is.

Wenn een 'n Ruut konstruieren will, denn bruukt een twee Informatschonen:

• de Siedenläng a
• een vun de twee Winkels

Formeln für de Ruut
Flach	$A\,=\,{\frac {1}{2}}\cdot e\cdot f={\frac {1}{2}}\cdot {\overline {AC}}\cdot {\overline {BD}}$
Flach	$A\,=\,a^{2}\cdot \sin \alpha =a^{2}\cdot \sin \beta$
Ümfang	$u\,=\,4\cdot a$
Läng vun de Diagonaal	$e\,=\,2\cdot a\cdot \cos {\frac {\alpha }{2}}=2\cdot a\cdot \sin {\frac {\beta }{2}}$
Läng vun de Diagonaal	$f\,=\,2\cdot a\cdot \sin {\frac {\alpha }{2}}=2\cdot a\cdot \cos {\frac {\beta }{2}}$
Radius vun’n Binnenkreis	$\rho \,=\,{\frac {1}{2}}\cdot a\cdot \sin \alpha$
Läng vun een Siet	$a\,$
Grött vun den Binnenwinkel bi A	$\alpha \,$
Grött vun den Binnenwinkel bi B	$\beta \,$
Längt vun de Diagonalen	$e={\overline {AC}};\quad f={\overline {BD}}$

De Ruut warrt in de Heraldik faken bruukt.